
A. 覚えやすいゴロを考えましたので、ご参考にしてください。
三角関数の加法定理は、そのものの利用機会が多い上に、三角関数の他の公式のもととなる最重要公式である一方、丸暗記しづらく導出も面倒くさいため、語呂合わせで覚えるのが最適です。
以下の語呂合わせで覚えましょう。
sin(α+β) バージョン
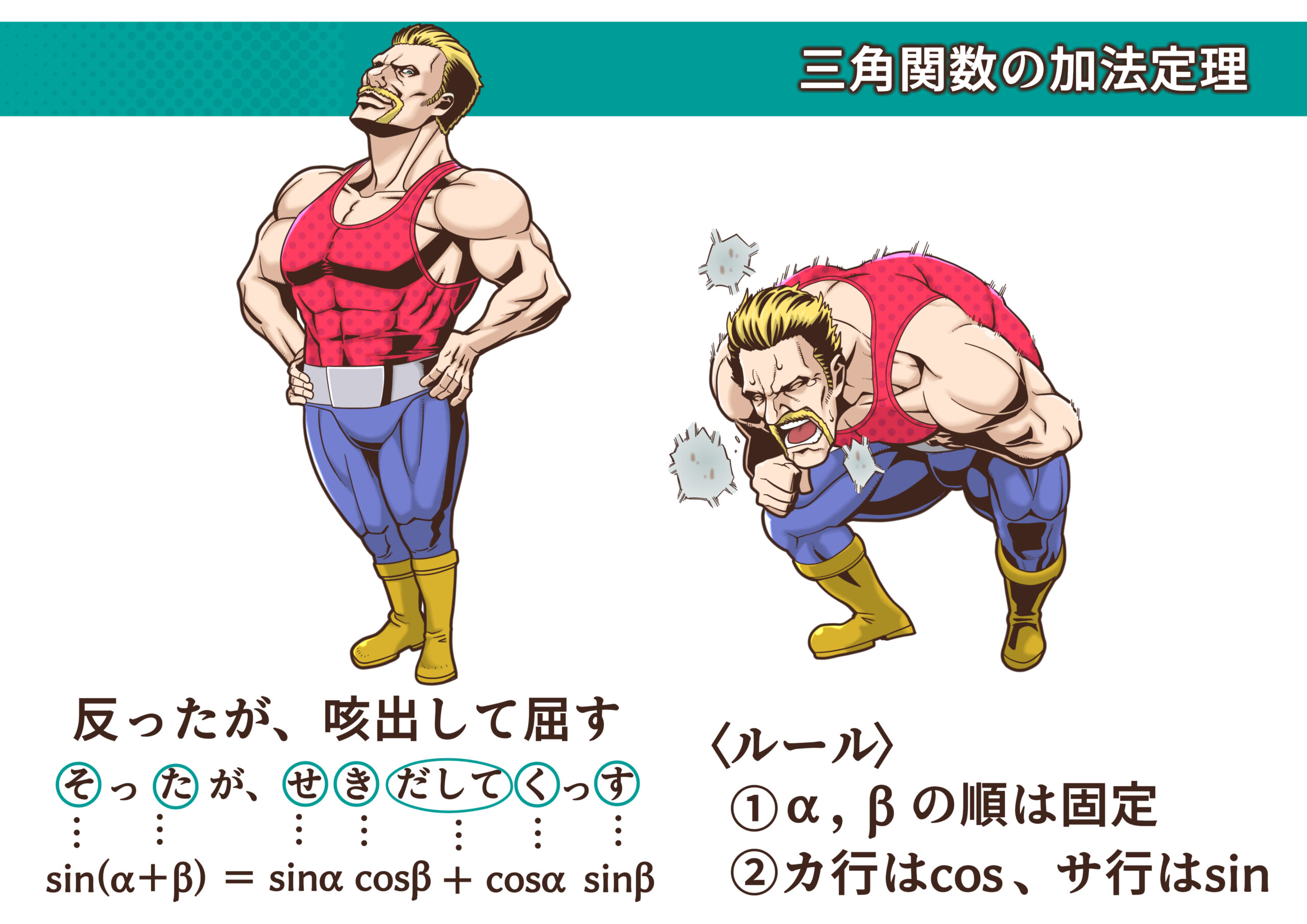
cos(α+β) バージョン
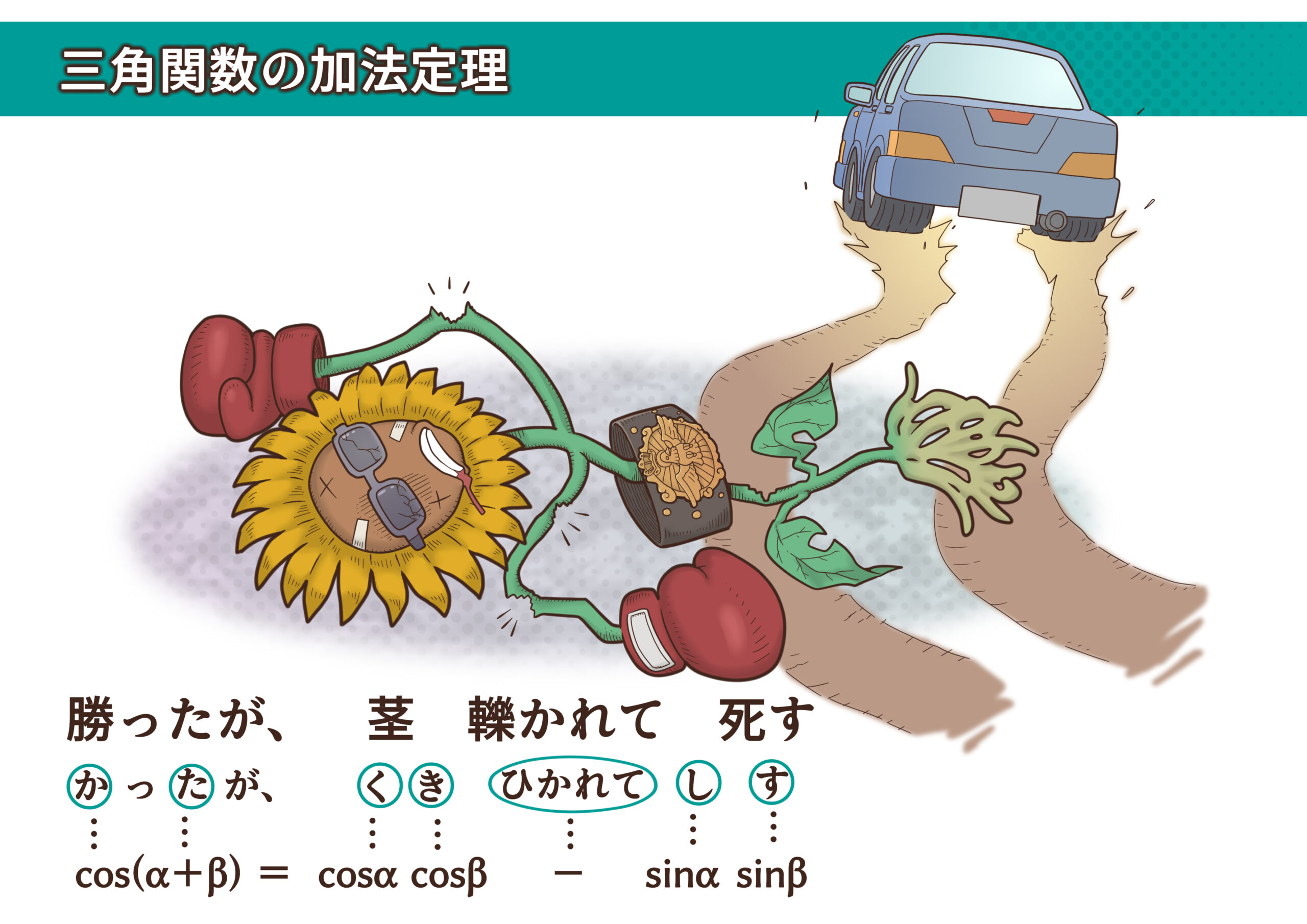
加法定理を使った公式の導出方法
三角関数の加法定理を覚えれば、
・三角関数の積和公式
・三角関数の和積公式
・三角関数の2倍角、3倍角、半角公式
・三角関数の180°-θ公式
・三角関数の90°-θ公式
・三角関数の90°+θ公式
などが導出できます。単に加法定理に代入するだけで導けます。
三角関数の加法定理とは? 基本を理解しよう
三角関数の加法定理とは、便宜的な説明をすると、「三角関数内の和を分解すること」と言えます。sin(α+β)を、sinα, sinβ, cosα, cosβ を使って表現することです。
三角関数を学ぶ上での重要ポイント
三角関数を学ぶ上で押さえておきたいポイントは、三角関数によらず⚪︎⚪︎関数と名のつくものは、二次関数や三次関数に帰着させて解くものが多いということです。よって、下地となる数1の二次関数や、数2の微分法などはきちんと学ぶ必要があります。
三角関数の分野でもっとも難しい問題は「三角方程式の解の個数問題」です。三角方程式は、二次方程式や三次方程式に帰着させて解くことが多いのですが、t=sinθ などと置換した際、tの解の個数とθの解の個数の対応を考えなければならないからです。
こういった問題は網羅系問題集(『Focus Gold』『青チャート』『ニューアクションレジェンド』など)に基本的に載っているので、必ずできるようにしたいです。逆に言えば、この手の問題が解けるようになっていれば三角関数はマスターしたといっても過言ではありません。
加法定理を活用した問題演習
『Focus Gold』『青チャート』『ニューアクションレジェンド』等の教科書傍用問題集に載っている問題をやれば、計算問題や基本操作から典型問題までひと通り触れることができます。これらで偏差値67.5(全統記述模試)までは固く取得可能です。
受験勉強における三角関数の位置づけ
二次関数の発展版であり、三角比の発展版であり、微積分の下地となる分野です。非常に重要なトピックとなので、『Focus Gold』『青チャート』『ニューアクションレジェンド』で徹底的に潰しましょう。
効率的な三角関数の学習法
計算問題や基本操作、典型問題を網羅することが必要十分な学習となります。シンプルに『Focus Gold』『青チャート』『ニューアクションレジェンド』等の教科書傍用問題集に載っている問題が自力で解けるようになれば完了です。
解けた問題には⚪︎マーク、解けなかった問題には×マークをつけ、解けなかった問題だけ復習できるようにしておくと無駄な学習が減り効率的です。また、一度解けた問題はできるだけ放置したほうが、たとえ忘れたとしても思い出す過程で定着するため、分散学習となり効率的です。

